阿基米德在公元前 3 世纪就研究了用于计算面积的积分，牛顿和莱布尼茨在 17 世纪才想出微分的方法。二者中间相差了1800年以上的时间。

01为何先从积分开始？

几乎所有的大学数学教科书都先说明微分后再引入其逆运算—不定积分。而且，用于计算面积的定积分被定义为不定积分的差。虽然按照上述顺序有逻辑地教授数学当然合乎情理，但历史上的发展顺序恰好相反。阿基米德在公元前3世纪就研究了用于计算面积的积分，牛顿和莱布尼茨在 17 世纪才想出微分的方法。二者中间相差了1800年以上的时间。

在历史上积分先被发现，这其中存在一定原因。积分与面积、体积等具体量的计算有着直接的关系。另外，研究微分前，首先必须准确地理解无穷小和极限等概念。例如物体运动的速度需要通过微分定义，不过因为在古希腊时期并没有确定极限的概念，所以出现了芝诺的“飞矢不动”悖论。

我认为在学习复杂的微分前，最好还是正确把握从直觉上相对容易理解的积分，再来思考其逆运算微分。因此，先解释积分。不管你是在大学的微积分课上听得不明不白，还是正在打算开始学习微积分，都可以试着“先从积分开始”。

02面积究竟如何计算

积分是从计算图形面积开始的。面积的单位包括平方米、平方千米等，即都带有“平方”二字。边长为1米的正方形面积等于1平方米。也就是说，面积是以正方形作为单位，计算图形的面积相当于几个正方形。如果是长方形，该如何计算面积呢？在小学阶段，我们就学过长方形的面积是长和宽的乘积，不过现在我们先假装没有学过这个计算公式。

假设已知长方形宽 1 米，长 2 米，那么竖着从正中间将长方形分成两个部分，就得到两个边长为 1 米的正方形，所以长方形的面积就等于 2 平方米。也就是说，长和宽的乘积等于长方形的面积。

接下来再假设 n 和 m 均为自然数，已知长方形宽 n 米，长 m 米，那么只要宽被等分成 n 部分，长度被等分成 m 部分，就能得到 n × m个边长为 1 米的正方形（图 7-2）。该长方形的面积正好等于正方形面积的 n × m 倍，即 n × m 平方米。结果还是等于长和宽的乘积。

 

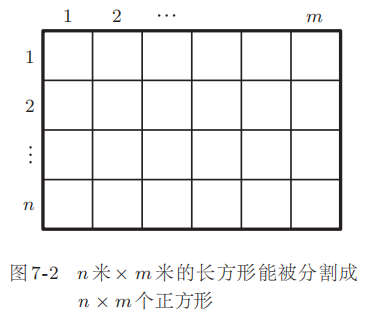
即使长和宽的值是分数，只要使用近似值，就能推算出等于整数的长方形面积，其面积依然等于长和宽的乘积。另外，只要考虑到极限，即使长和宽的值是类似（根号2）的无理数，也能用长和宽的乘积来计算面积。

我们在小学还学过三角形的面积等于“底乘以高除以 2”。如图 7-3 所示，如果将三角形的面积增加一倍，那么就等于长方形的面积。

3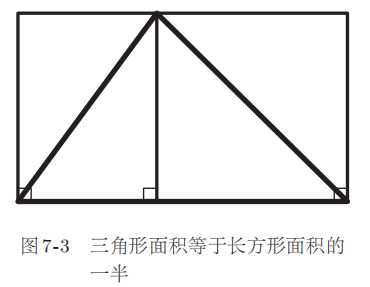 

不仅是长方形和三角形，只要是折线围成的图形，不管是什么形状，古希腊人都能找出其面积与三角形面积的关系。正如图 7-4 所示，折线围成的图形即使是不规则的图形，也能用三角形集合来表示，所以只要计算出所有三角形的面积，将计算结果相加就能得到该图形的总面积。

4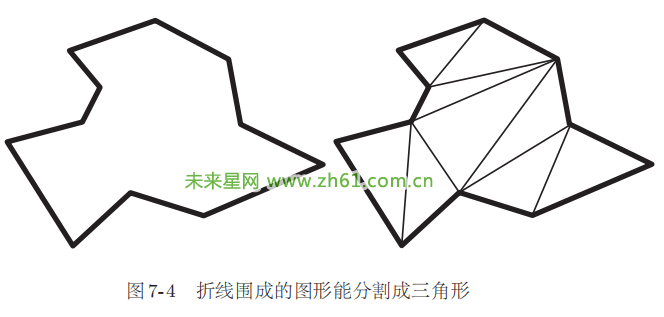 

03如何计算任何形状都 OK，阿基米德的夹逼定理

现在我们已经知道，只要是折线围成的图形，就能将其分割成三角形后再计算面积。那么，如果是光滑曲线围成的图形，例如抛物线和圆等，其面积又该如何计算呢？关于这个问题，我们马上就能想到将曲线近似为折线，如图 7-5 所示。所以求曲线围成的图形面积时，只要计算折线图形的近似面积即可。

5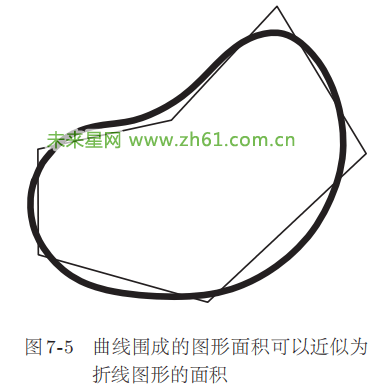 

虽然这个想法不错，不过因为近似总是带有误差，所以有必要估算误差的大小。如果可以的话，尽可能将误差降至 0。这个时候，我们先来解释阿基米德研究出来的“方法”。

如图 7-6 所示，假设已知曲线围成的图形 A，首先在图形A 中画出折线围成的图形 B。然后再画出一个围在图形 A 外侧的图形 C。上述三个图形之间成立一个不等式，即面积 (B) ≤面 积 (A) ≤ 面 积 (C)。我 们 暂时无法正确计算出图形 A 的面积，不过图形 A 的面积大于图形 B 的面积（因为是折线图形，所以可以计算），同时小于图形 C 的面积（因为也是折线图形，所以可以计算）。因此，我们就得出折线图形的近似误差。

6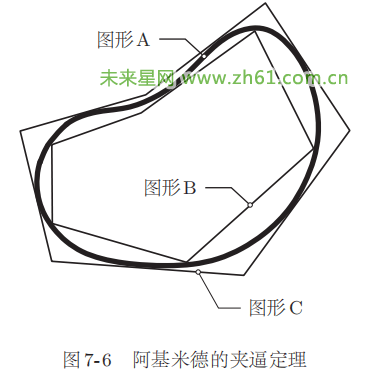 

不过，怎样才能将误差降至 0 呢？阿基米德想到的方法是不仅限于一组折线图形 B 和 C，而是如图 77 所示的那样增加顶点数量，使得折线图形不断接近曲线图形 A。因此，这些折线图形可以记作

在每一组图形中，图形 A 包含图形 Bn，同时又被图形 Cn所包含。那么，

三者之间的关系与之前相同，即

7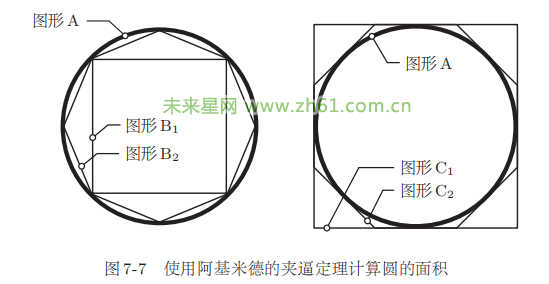 

图形组(Bn、Cn)的数值越大，近似值就越精确。近似值越精确就代表图形Bn和图形Cn的面积越接近图形A的面积。不过，我们并不知道图形A的面积有多大。那么我们又如何能保证折线图形的面积会不断接近未知的面积呢？

阿基米德认为，在n不断变大的过程中，

的值会不断变小。所以当 n 是无穷大时，上述公式的差将等于 0。因为图形 A 的面积介于面积 (Bn) 和面积 (Cn) 之间，所以两者均达到极限时的值应该就是图形 A 的面积。据说阿基米德通过借鉴公元前 4 世纪的数学家欧多克索斯的理论，从而研究出了上述方法。因为阿基米德用上述方法成功解决了几何学上的许多问题，所以该方法被称作“阿基米德的夹逼定理”。

接下来我们举例说明如何计算圆的面积。如图 77 所示，(B1、C1) 是正方形，(B2、C2) 是正八边形，可以推测 (B3、C3) 是正十六边形，那么 (Bn、Cn) 就是正

边形。使用 (Bn、Cn) 近似圆的面积。

用连接圆心和顶点的直线可以将图形 Bn 和图形 Cn 分割成三角形集合。我们可以发现，n 的值每增大 1，两者的面积差

就会减小至一半以下。n的值越大，误差就依次减半，越来越小。因此，当n是无穷大时，面积(Cn)和面积(Bn)的值正好相等，而且这个值就等于圆的面积。这就是阿基米德计算圆的面积的方法。

04积分究竟计算什么

使用阿基米德的夹逼定理，能计算更复杂的曲线图形的面积。用笛卡儿坐标表示的话，如图78所示，直线可以表示为y=ax+b，抛物线表示为

8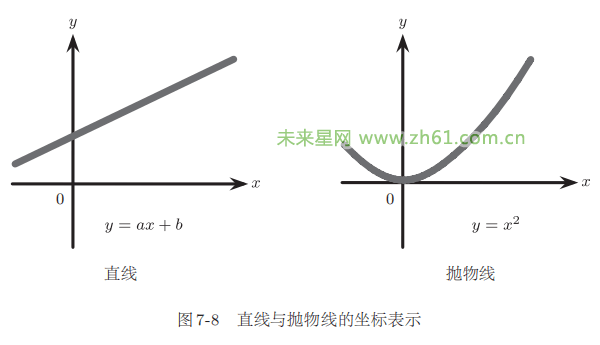 

假设已知某函数f(x)，那么我们来思考一下曲线y=f(x)。如图7-9所 示，假 设 在 区 间a≤x≤b上f(x)的值始终大于0，那么我们来研究一下曲线y=f(x)和y= 0、x=a、x=b这三条直线围成的图形A（图中的阴影部分）。如果知道如何计算图形A的面积，就能通过拼组的方法计算任何曲线围成的图形面积。

9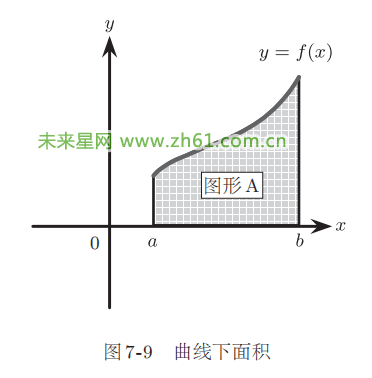 

曲线y=f(x)沿着y轴方向上升或下降。为了便于计算，假设在区间a≤x≤b上，y=f(x)一直在增大。在其他情况下，将区间a≤b分成两部分，即f(x)不断增大的区间和f(x)不断减小的区间。只要将以下方法分别代入上述两个区间即可。

为了用阿基米德的夹逼定理来计算图形A的面积，首先将区间a≤x≤b分成n部分，如图710中的图形Bn和Cn。图形A包含图形Bn，同时被包含在图形Cn中。图形Bn和Cn均是长方形集合，所以能够计算出面积。

10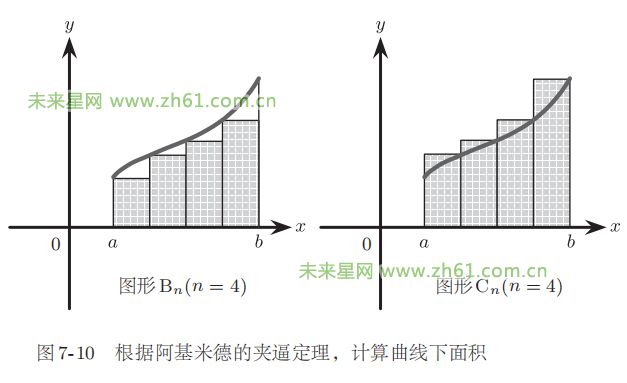 

如图711所示，面积(Cn)和面积(Bn)的差等于

也就是底ε= (b−a)/n、高= (f(b)−f(a))的长方形的面积。n的值越大，ε的值就越小，因此图形Bn和图形Cn的面积就越接近。当ε的值达到极限即等于0时，两个图形的面积相等。达到极限时的值也就是图形A的面积。

按照上述方法计算的图形A的面积叫作“函数f(x)在区间a≤x≤b上的积分”，用公式记作

11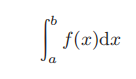 

与牛顿同时创立微积分法的莱布尼茨发明了符号

是“求和”(sum)的首字母“S”的拉长。而且，“dx”的 d 是指“求差”(difference)的首字母。当将图形近似为长方形集合时， 一个长方形的底长等于 x + ε 和

12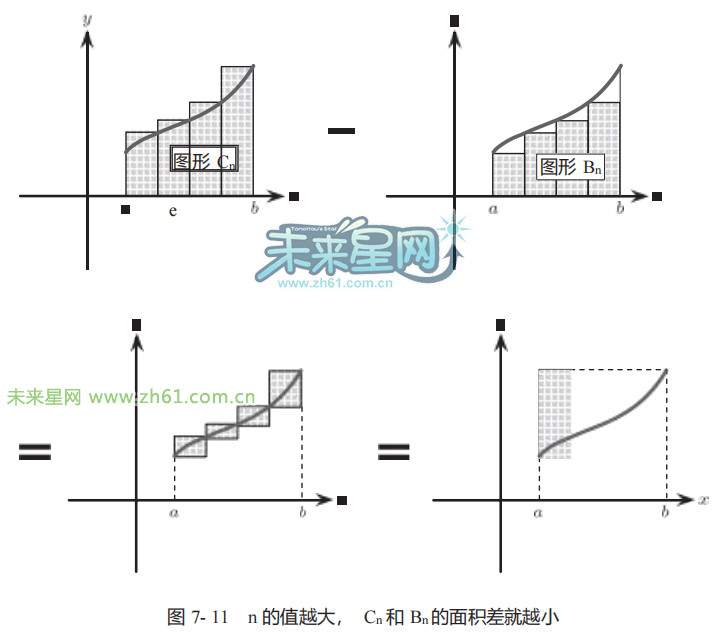 

x 的“差”。高为 f(x)、底为 e 的长方形面积等于 f(x)e， 因此可以用符号 dx 代替 e，即 f(x)dx。也就是说，

中包含着莱布尼茨的想法， 即“积分是指在 x = a 到 b 的区间上排列出高等于 f(x)、底为 dx 的长方形，并求出它们的面积之和”。

上文中解释的积分沿用了 19 世纪德国数学家波恩哈德 ·黎曼的定义，所以称作“黎曼积分”。其实积分包括许多类，例如法国数学家亨利 ·勒贝格提出的“勒贝格积分”、日本数学家伊藤清提出的“伊藤积分”等。黎曼积分足以处理我们在高中所学的函数问题，不过当我们需要处理类似股票价格等随机波动的数值时，则需要用到伊藤积分。伊藤积分还被用于决定期权的价格， 因此伊藤清被认为是“在华尔街最有名的日本人”。

05积分与函数

我们再来根据黎曼的定义计算各种积分。首先， 如果求一次函数 y = x 在区间 x = 0 到 x = a 上的积分， 结果会如何？如图 7- 12所示， 这是一个底为 a、高为 a 的直角三角形的面积， 所以应该等于 a2/2 。接下来我们来验算一下。此 时，图 形 Cn 是 底 长 为ε = a/u、高为 ε,2ε , ··· 的长方形集合，那么

13 

从毕达哥拉斯那个时候起，人们就知道如何计算 (1 + 2 + ··· + n) 的值。计算时，先将其乘以 2，即

14 

等式右边第 1 个方括号中的第 1 项是 n，第 2 个方括号中的第 1 项是 1，因此两项的和等于 (n + 1)。两个方括号中的第 2 项分别是 (n − 1) 和 2，两项的和也等于 (n + 1)。等式右边总共有 n 个和等于 (n + 1) 的组合，因此右边就等于 n × (n + 1)。因为左边乘以 2，所以最后要除以 2，即

代入上述公式，即

15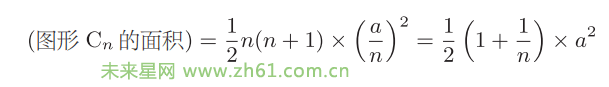 

n 的值越大，括号中的 1/n 的值就越能忽略。因此当 n 为无穷大时，面积就等于

结果与直接用三角形计算的面积相等。用积分符号表示的话，即

16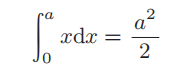 

求二次函数

在区间x= 0到x=a上的面积也使用同一个方法，不过详细解释起来计算过程有点长。阿基米德在公元前3世纪就发现了二次函数的积分公式，因此不解释又太可惜了。那么我就简短地解释一下。在二次函数y=x2的情况下，图形Cn是底长为ε=a/n、高为ε2, (2ε)2,···的长方形集合，即

17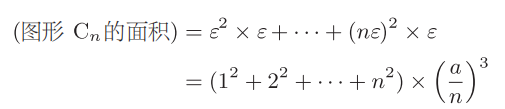 

此处出现的和可以计算为

那么

18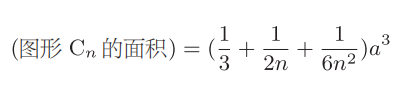 

因此当 n 为无穷大时，可以计算积分

19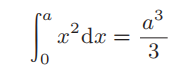 

详细说明请参考本书附录中的补充知识。使用相同的方法，还能计算更高次函数的积分。计算

在区 间 x = 0 到 x = a 上的积分时，必须先计算

1636 年，因“费马大定理”而名声大噪的费马在给朋友的信中提到，因为

20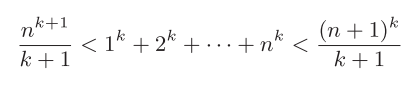 

所以能计算

的积分。其实只要使用上述不等式和阿基米德的夹逼定理，就能得出

21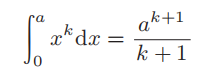 

最后欧拉证明了关孝和与伯努利的公式。由于当时日本采取锁国政策，因此欧拉无从得知关孝和的业绩。正因为如此，他将上述公式中的系数称作伯努利数，这个叫法一直沿用至今。既然关孝和与伯努利独立发现了上述公式，那么应该称之为关 - 伯努利数。

06飞矢不动？

积分与面积和体积的计算有关，而微分则与速度的计算有关。既然要思考速度，那芝诺又要出场了。

我们思考一下离弦之箭的情况。时间是瞬间的集合，那么离弦后的箭在飞行过程中的任何瞬间都处于一个固定位置。既然是固定位置，那就和不动没有什么区别，因此“飞矢不动”是一个悖论。当然，上述命题听起来十分愚蠢。那么到底哪里出错了呢？

首先我们来反思一下速度是什么。假设 1 小时能步行 3.6 千米，那么速度就为 3.6 千米/小时。速度是指移动的距离除以所花费的时间，即

如果再次缩短时间，即

速度就变为了 1 米 / 秒。随着时间的缩短，移动的距离也会变短，如果保持相同的移动速度，那么时间与距离之比也不会发生变化。只要时间逐渐缩短至 0 即达到极限，应该就能定义某个瞬间的速度。

假设在直线上从左向右移动，用直线的坐标 x 来判断位置。将时刻 t 所在的位置记作 x(t)，从时刻 t 到 t′ 的区间内只移动了 (x(t′) −x(t))。移动时的平均速度等于 (x(t′) − x(t)) ÷ (t′− t)。因此，如果 t′不断向 t 靠近，那么在极限 t′= t 时应该能够计算出时刻 t 的速度。不过，因为在极限的情况下 x(t′) − x(t) 和 t′− t 的结果均等于 0，所以如果计算 0 ÷ 0，那么计算过程就变得莫名其妙。计算时需要注意。假设 x(t) = t，那么

之所以在极限的情况下很容易出现 0 ÷ 0 的错误，是因为分子和分母都存在 (t′− t)。不过只要事先将双方的 (t′− t) 相抵消，即使假设 t′= t也不会出现任何问题。

接着思考一下 x(t) = t2 时的情况，即

22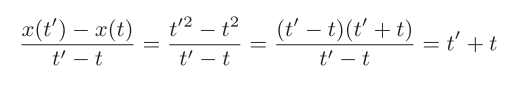 

上述公式中的分子和分母抵消了 (t′− t)。抵消后，假设 t′= t，那么速度等于 2t。也就是说，速度和 t 成正比。

为了计算某个瞬间的速度，思考 (x(t′) − x(t)) ÷ (t′− t) 中 t′→ t的极限时，容易出现 0 ÷ 0 的问题。不过之前的例子已经表明，只要先抵消分子和分母中的 (t′− t) 后再求极限，就不会出现任何问题。用微分的定义可以表示为

等式右边的符号 lim 是“limit”（极限）的意思。虽然英国的牛顿和德国的莱布尼茨独立发现了微分，不过与积分一样，微分的表达方式 dx/dt也是由莱布尼茨所发明。

回到芝诺的悖论，其中的问题在于

23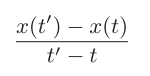 

以及如何计算 t′→ t 的极限。如果随意计算分子和分母的极限，容易引发悖论。如果先假设分子 x(t′) − x(t) 等于 0，那么上述算式就是0÷ (t′− t)，之后不管分母 (t′− t) 的值多小，算式都等于 0。这就是“飞矢不动”的根本含义。也就是说，芝诺的悖论错在处理极限的方法。不是要单独思考分子和分母的极限，而是将 (x(t′) − x(t)) ÷ (t′− t) 的分子和分母看成一个整体，对其计算 t′→ t 的极限，“瞬间的速度”才具有意义。从芝诺的时代到牛顿和莱布尼茨真正理解其中含义，中间大约相隔了 2100 年的时间。

07微分是积分的逆运算

微分是积分的逆运算，这是牛顿和莱布尼茨最重要的发现之一。假设已知函数 f(x)，f(x) 在 0 到 a 的区间上的积分表示为

可以将其看作 a 的函数。再对 a 微分得到

代入原函数 f(x)，即 x = a。这意味着微分是积分的逆运算。接下来进行证明。如果图形 A 可以被分为图形 B 和图形 C，即

假设图形 A 是曲线 y = f(x) 下面的区间 0 ≤ x ≤ b。将该区间分成两部分，即 0 ≤ x ≤ a 和 a ≤ x ≤ b。那么面积也被分成

24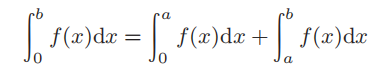 

因此，将等式右边的第一项移至左边，得到

25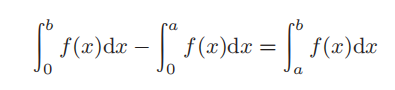 

将上述等式代入微分的定义中，那么

26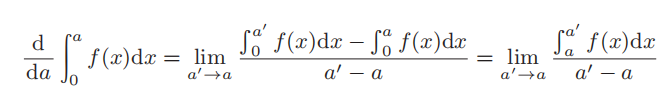 

为了计算微分，使 a′的值不断变小并趋近 a，那么在短区间 a<x<a′上，f(x) 的值几乎不变。因此积分

可以近似等于底为 (a′− a)、高为 f(a) 的长方形面积，即

27 

将上述公式代到上面的公式中，得到

28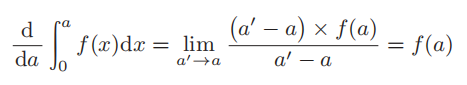 

我们可以发现，对积分进行微分后又重新回到了原函数。反之，如果对函数进行微分后再进行积分，那么又会回到最初的状态。

29

牛顿和莱布尼茨的“微积分学基本定理”指的就是微分和积分是逆运算。在日本的高中教材中，通常先定义微分，然后再定义积分是其逆运算。所以在日本的高中数学中，“微积分学基本定理”不是定理，而是积分的定义。在本章中，我们已经将积分定义为“曲线 y = f(x) 的曲线下面积”，所以“微积分学基本定理”就是一个定理。

08指数函数的微分与积分

与积分相比，微分是更高级的数学概念，更需要注意处理极限的方法。尽管如此，日本的高中仍然先教微分，原因之一在于微分的计算相对比较简单。使用自然常数 e 的指数函数

接下来我们计算一下该指数函数的微分，首先将其代入微分的定义，得到

30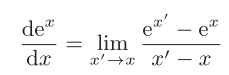 

指数函数具有以下性质：

使用上述公式，等式右边的分子等于

31 

因此指数函数的微分可以表示为

32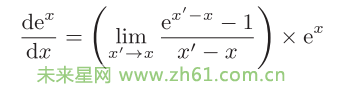 

假设等式右边的 x′− x = ε，那么 x′→ x 的极限等于 ε → 0。所以

上述等式右边的极限值为

证明过程虽然简单，但仍然需要计算。因此，详情请参阅本书附录中的补充知识。使用上述公式，我们可以发现指数函数 ex的微分是其本身。

既然能够计算微分，那么根据“微积分学基本定理”就能简单地计算积分。首先，分别对上述微分公式的两边进行积分，即

33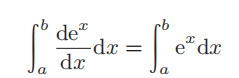 

在上述等式的左边使用基本定理，得到

因此，

不用借助微分，就能使用定理直接计算指数函数的积分。详情请参阅本书附录中的补充知识。阅读完以后，你会发现与微分相比，积分的计算有多么复杂！

对于三角函数 sin x、cos x 和 tan x，积分也能作为微分的逆运算进行计算。

对于指数函数、三角函数等高中阶段学习的函数，微分的计算比积分简单。但是，除幂函数、指数函数和三角函数以外，能够精确计算微积分的函数非常少。出现在数学应用中的函数，虽然其中也有一些能够使用上述三种函数中的其中一种函数进行近似，不过大多数的函数只能通过计算机进行数值计算。

虽然懂得如何计算指数函数和三角函数的微积分会有帮助，但作为必须要掌握的知识，微分和积分显得尤为重要，因此首先要正确理解微分和积分所包含的意思。正因为如此，本章的内容才从积分开始谈起。